In our previous blog post, we discussed the overall working of the Mareekh Process; from the extraction of liquid water from permafrost or subsurface glaciers, its heating in two separate feeder systems, channelling the superheated steam through the turbine, and recovery of condensate, to the extraction of a net amount of energy from the whole process utilizing the unique attributes of the Martian atmosphere.
Mareekh Process is our patented hybrid power generation technology inherently designed to work in a unique Martian context providing reliable power solutions for a large-scale permanent human settlement on Mars. It is hybrid since the process will be kickstarted using auxiliary power such as solar or limited nuclear to extract liquid water from subsurface ice deposits and generating power using the low atmospheric temperature and pressure as a heat sink. The net gain of power will make this process self-sustained throughout its operation cycle.
The net gain of power from subsurface ice requires explanation based on the laws of thermodynamics. It also requires revisiting the very definition of fuel itself.
What is fuel?
What makes something a fuel? In a simplistic way it can be defined as a substance that can be converted into another substance either spontaneously or with a small activation energy, giving out a net energy in that process which can be utilized to do work.
Common examples of fuel are coal, wood, gasoline, natural gas, even radioactive material. They can be spontaneously converted into products at much lower energy levels usually through an activation energy input, giving out heat and utilizing it for work.
Should we remain limited to this definition of fuel? Can the water stored in a dam be considered fuel? After all it lets us do work when it flows from a height by turning the blades of a turbine yet without any change in its chemical composition. What is common between water flowing down a dam and coal burning in the air that makes them useful for performing work? It is not strictly the chemical composition but the ability to change the entropy of the system from low entropy (high order) to the higher entropy (lower order or higher disorder). We don’t actually use energy. Energy can change its form but it can never be used up. We use the order of the system from a higher order to lower order and extract work in the process. In other words, the work can be extracted when a system moves from a lower entropy to a higher entropy. Entropy of the universe always increases. This is why water cannot used as a fuel in a car if any model claiming to achieve this through a chemical conversion of water into by-products with a decrease in the entropy of the system as this conversion is highly endothermic i.e. requires external energy to decrease the entropy of the system and not the other way round. So the common factor between a burning piece of coal and water flowing down a dam is the increase in entropy of the universe, and the utilization of this transition to do work.
Now imagine a chunk of coal on a table. It will slowly oxidize with oxygen in air and give out CO2 and heat even at room temperature without giving any extra activation energy and will completely convert into CO2 and ash over a very long period of time. Can it still be considered a fuel despite the fact that such spontaneous conversion cannot be utilized to perform work? On the other hand, imagine water flowing down in wetlands at extremely slow speeds (few centimeters per minute). Can it be utilized to extract useful work through turbines? The answer is no in both scenarios, even though both processes are increasing the entropy of the system, but not quick enough to be useful. So the prerequisite for anything to be a source of power to perform work is its ability to change the entropy of the system rapidly enough.
In the Mareekh Process, we are aiming to rapidly convert the water stored in subsurface glaciers and permafrost into a steam of very high entropy when exposed to the very deep heat sink of the Martian atmosphere. This can be achieved by giving an activation energy to the stored subsurface ice through auxiliary means such as solar or limited nuclear.
The concept of Gibbs Free (Available) Energy
The concept of Gibbs Free Energy is deeply intertwined with the second law of thermodynamics which states that entropy of the universe always increases in a spontaneous process. And what drives this spontaneity of a process from a higher order (low entropy) to lower order (high entropy) is the Gibbs free or available energy.
In Mareekh Process, the end products (exit steam and the condensate) are subject to the two key components of the spontaneity matrix of the Gibbs reaction (Figure 1), that is, decrease in enthalpy and increase in entropy (inherently spontaneous at all temperatures, i.e. the process of formation of exit steam that starts at the turbine inlet) and the decrease in enthalpy and entropy (spontaneous at lower temperatures i.e. the formation of condensate at the end of the turbine housing). Also considering the entire Martian atmosphere acting as an infinitely big “surface condenser” with extremely low pressures and temperature with the exit valve of the turbine housing acting as its inlet, the efficiency of the Mareekh process is further increased.
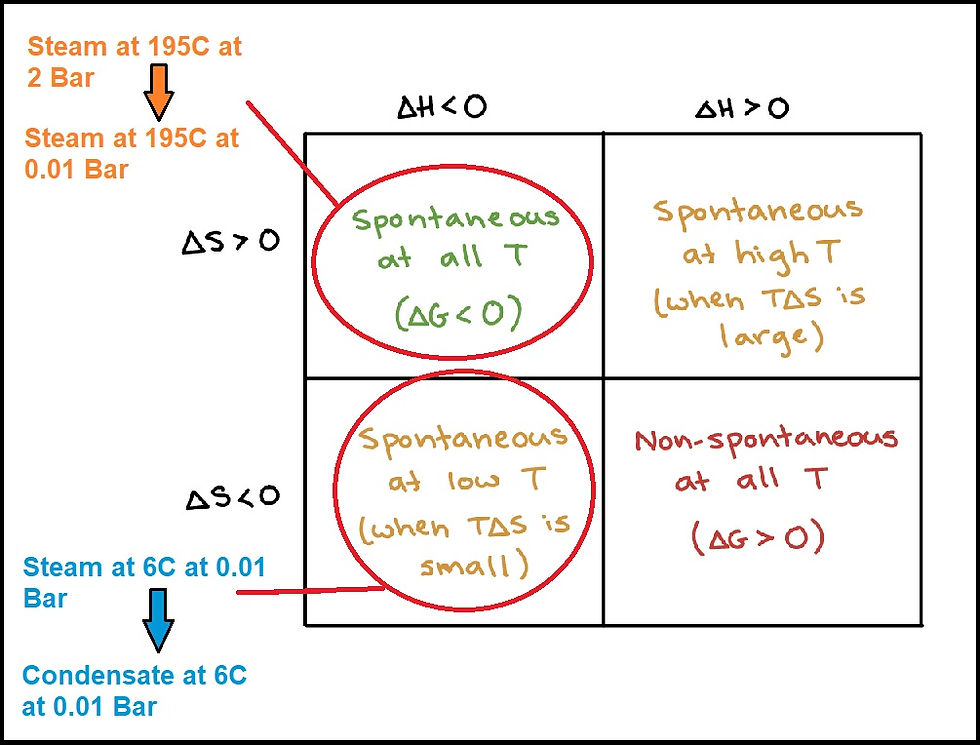
Figure 1: Gibbs Free Energy and spontaneity of a reaction. (Diagram modified from www.khanacademy.org/science/chemistry/thermodynamics-chemistry/gibbs-free-energy/a/gibbs-free-energy-and-spontaneity)
Figure 2
(Source:www.khanacademy.org/science/biology/energy-and-enzymes/free-energy-tutorial/a/gibbs-free-energy)
The energy input
The entire energy expenditure of 2710kJ is for the creation of 1.5kg of superheated steam at 195C at the turbine inlet (Figure 3). The steam at 195C is well above saturation temperature for 2 bar (which is around 113C) converting it into an “explosive mixture” which, according to the spontaneity of the reaction, is spontaneous at all temperatures due to negative Gibbs Free Energy (ΔH<0, ΔS>0) (Figure 1)
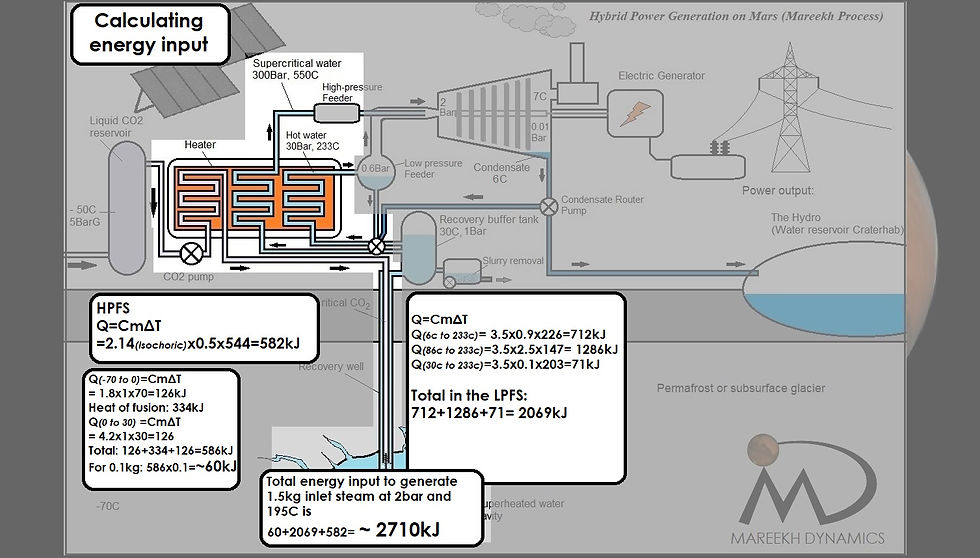
Figure 3: Total energy input in all the steps to generate 1.5kg of superheated inlet steam at 2bar
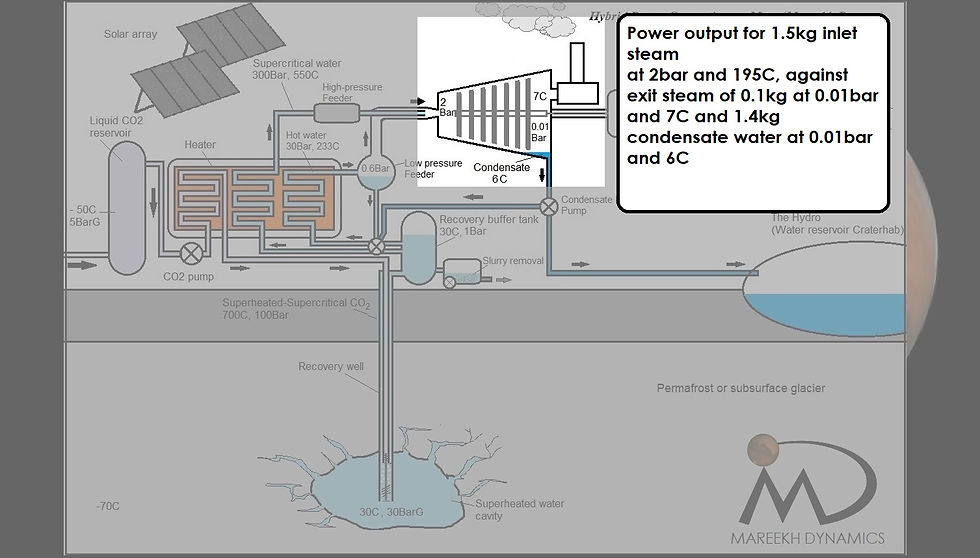
Figure 4
The power output
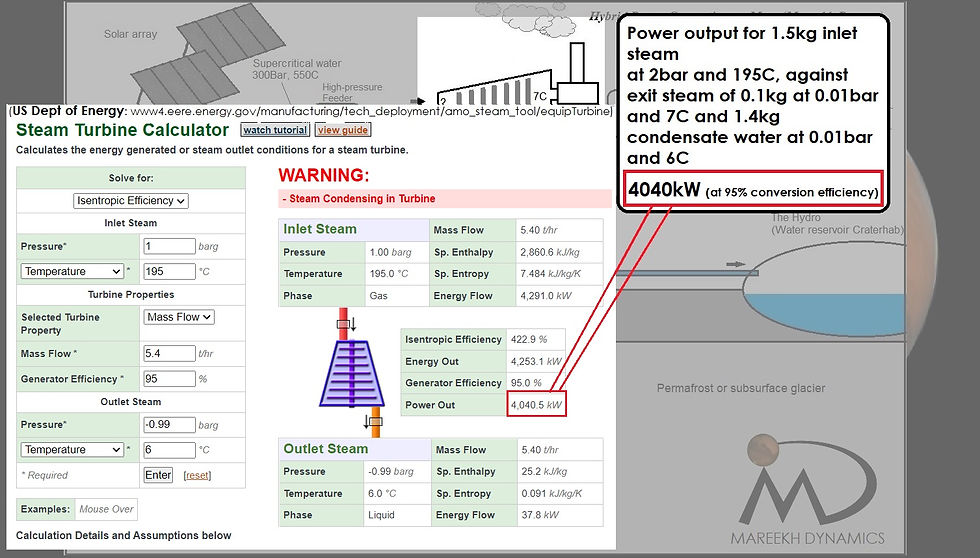
Figure 5: Power output calculation for superheated steam at 195C and 2bar to condensate at 6C and 0.01bar
As per the US Department of energy steam turbine calculator, this steam will eventually generate a power of 4253 kJ/s (4040kJ/s for 95% conversion efficiency) during its conversion to the condensate at 6C at 0.01bar.
Analysis of the power output
Let’s break down the power output into its individual components.
During the conversion of superheated steam of 195C at 2 bar pressure (created from mixing of the supercritical water from HPFS and the saturated flash steam from LPFS) to the condensate at 6C at 0.01bar (+ exit steam), the following thermodynamic events happen.
1. Exposure of superheated steam at 195C at 2bar to 0.01bar
2. Expansion work of the superheated steam from 195C at 2bar to condensate at 6C at 0.01bar
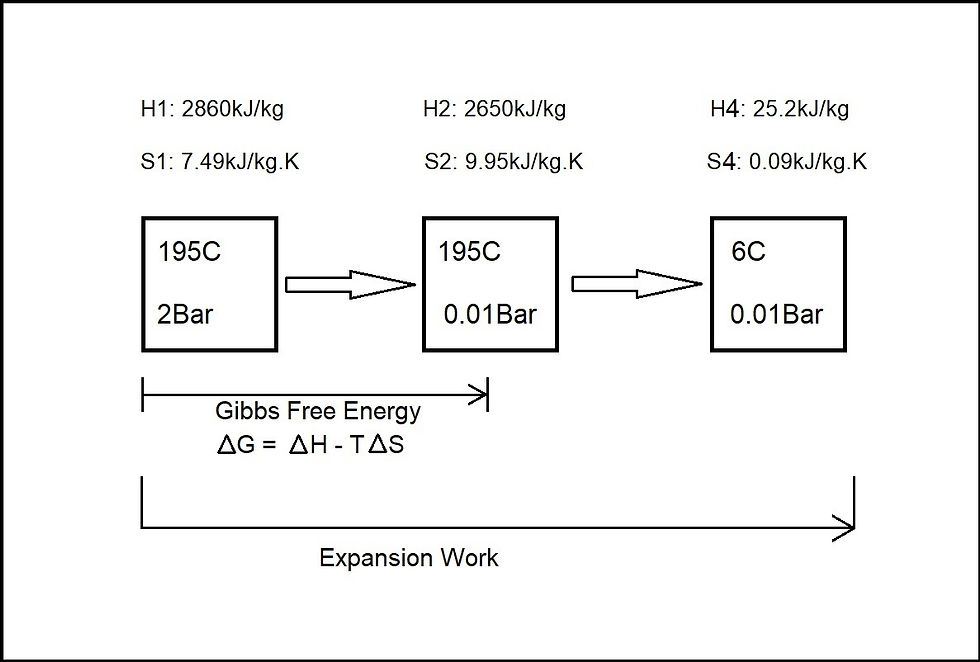
Figure 6: A breakdown of the power output
H = Enthalpy, S = Entropy
Conversion 1 which is a part of the total expansion work of steam for the given parameters, is mostly driven by the drop in enthalpy and rise in entropy. Its energy conversion to output can be calculated by the Gibbs Free Energy at the temperature of 195C or 468K
ΔG = ΔH - TΔS
For 1.5kg
Enthalpy of steam at 195C (468K) and 2 bar (H1) = 2860 x 1.5 = 4290kJ
Enthalpy of steam at 195C (468K) and 0.01 bar (H2) = 2650 x 1.5 = 3975kJ
Entropy of steam at 195C (468K) and 2 bar (S1) = 7.49 x 1.5 = 11.23
Entropy of steam at 195C (468K) and 0.01 bar (S2) = 9.95 x 1.5 = 14.95
Gibbs free energy of superheated steam of 468K and 2 bar converting at 280K to saturated steam at 0.01 bar pressure can be calculated as
ΔG = ΔH - TΔS
= (H2 - H1) - T(S2 - S1)
= (3975 - 4290) - 468 (14.95 - 11.23)
= -315 - 1740
= -2055kJ
The negative symbol is conventional to denote the amount of Gibbs Free Energy energy available in a system to do work, and represents spontaneity of the reaction.
It should be noted that this Gibbs Free Energy became available solely due the amount of entropy achievable by the superheated steam of 195C at 2 bar when exposed to a pressure of 0.01 bar. This energy is transferred to the turbine during the flow of the expanding steam through the turbine housing.
Calculating the Gibbs Free Energy for the same reaction in Earth’s atmosphere yields far less energy
Mareekh Process is specifically designed to work in a Martian environment (or any other planetary body with ice and very low atmospheric pressure and temperature, such as Europa, Ganymede, Callisto, or any other icy moons in the outer solar system, except Titan). It will not work on Earth or any other planetary body with high atmospheric pressure and temperature.
For 1.5kg
Enthalpy of steam at 195C (468K) and 2 bar (H1) = 2860 x 1.5 = 4290kJ
Enthalpy of steam at 195C (468K) and 1 bar (He) = 2870 x 1.5 = 4305kJ
Entropy of steam at 195C (468K) and 2 bar (S1) = 7.49 x 1.5 = 11.23
Entropy of steam at 195C (468K) and 1 bar (Se) = 7.81 x 1.5 = 11.7
ΔG = ΔH - TΔS
= (He - H1) - T(Se - S1)
= (4305 - 4290) - 468 (11.7 - 11.23)
= -15 - 220
= -235kJ
This is far lower than the Gibbs Free Energy for the same reaction on Mars (-2055kJ)
We can see that the same amount of superheated steam at 195C at 2 bar fails to release any significant amount of Gibbs free energy when exposed to Earth’s atmospheric pressures, which combined with the need for the energy rejection by the surface condenser to work (which won’t be required on Mars) makes a similar mechanism far less efficient on Earth than it is on Mars.
In order to make use of the Martian environment as a massive pressure and temperature sink, a connection to the exterior must be maintained. To avoid creation of a near-vacuum of the Martian atmosphere (0.006bar) inside the turbine’s low pressure housing and risking freezing of the condensate, a certain pressure must be maintained (0.01bar) inside the low-pressure turbine housing which can be achieved through a pressure-control exit valve. The pressure-control exit valve can also help achieve saturation temperature inside the low-pressure turbine housing as steam tends to expand to its saturation pressure and temperatures if allowed to expand unchecked. The pressure-control valve will determine the rate of exiting steam to the external near-vacuum of the Martian atmosphere and help achieve a desired pressure of 0.01bar (exterior pressure being 0.006bar). The enthalpy of exit steam (0.1kg/s in our model) will not get translated into mechanical work, reducing the net output work by a value equivalent to its enthalpy.
The total expansion work (2) is determined by the drop in enthalpy of the superheated steam of 195C at 2bar to the condensate at 6C, driven by the Gibbs Free Energy
Enthalpy of steam at 195C (468K) and 2 bar (H1) = 2860 x 1.5 = 4290kJ
Enthalpy of steam at 7C (280K) and 0.01 bar (H3) = 2510x1.4 = 3514kJ
Enthalpy of exit steam at 7C(280K) and 0.01bar (H3*) = 2510 x 0.1 = 251kJ
Enthalpy of condensate at 6C (279K) and 0.01 bar (H4) = 25.2 x 1.4 = 35kJ
Entropy of steam at 7C (280K) and 0.01 bar (S3) = 8.98 x 1.4 = 12.57
Entropy of condensate at 6C (280K) and 0.01 bar (S4) = 0.09 x 1.4 = 0.126kJ
ΔH = H1 - (H3*+H4) = 4290 - (251+35) = 4044kJ
A small amount of Gibbs Free Energy is also released during the conversion of end steam of 1.4kg to the condensate at 1.4kg
ΔG = ΔH - TΔS
= (H4 - H3) - T(S4 - S3)
= (35.3 - 3514) - 279(0.126 - 12.57)
= -3478 - 279(-12.44)
= -3478 + 3470
= -8kJ
4044+8 = 4052kJ
At 95% conversion efficiency: 4052 x 0.95 = 3849kJ
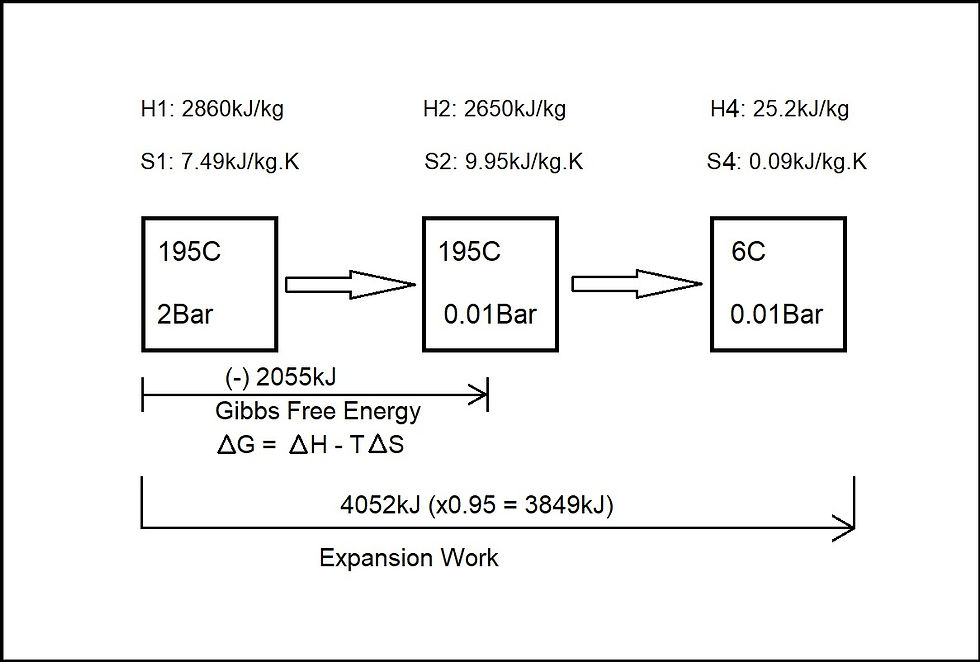
Figure 7
As the total input to achieve the 195C superheated steam at 2bar was 2710kJ as calculated earlier, the net output is 3849 - 2710 = 1139 ~ 1140kJ
The extra energy output can be explained by the large amount of Gibbs free energy which becomes available when superheated steam is exposed to the very deep heat and pressure sink of the Martian environment.
Conclusion
Mareekh Process is an interesting and game-changing concept in our quest for a reliable source of power using local resources on Mars to power a large-scale and permanent human colony. It proposes the use of the vast deposits of subsurface ice on Mars (permaforst or subsurface glaciers) to generate enormous amounts of clean energy utilizing the unique attributes of the Martian environment. It may be the ultimate single point solution for the power needs for a future human civilization on the red planet.

Comments